Trees depicted in the artwork of famous painters like Leonardo da Vinci and Piet Mondrian follow the math behind their branching pattern in nature, a new study says.
This hidden math in some abstract paintings may even underlie our ability to recognise such artwork as depictions of trees, according to the research, published in the journal PNAS Nexus.
Trees in nature follow a “self-similar” branching pattern called a fractal, in which the same structures repeat at smaller and smaller scales from the trunk to the branch tip.
In the new study, scientists mathematically examined the scaling of branch thickness in depictions of trees in artworks.
Researchers derived mathematical rules for proportions between branch diameters, and the approximate number of branches of different diameters.
“We analyse trees in artwork as self-similar, fractal forms, and empirically compare art with theories of branch thickness developed in biology,” researchers explained.
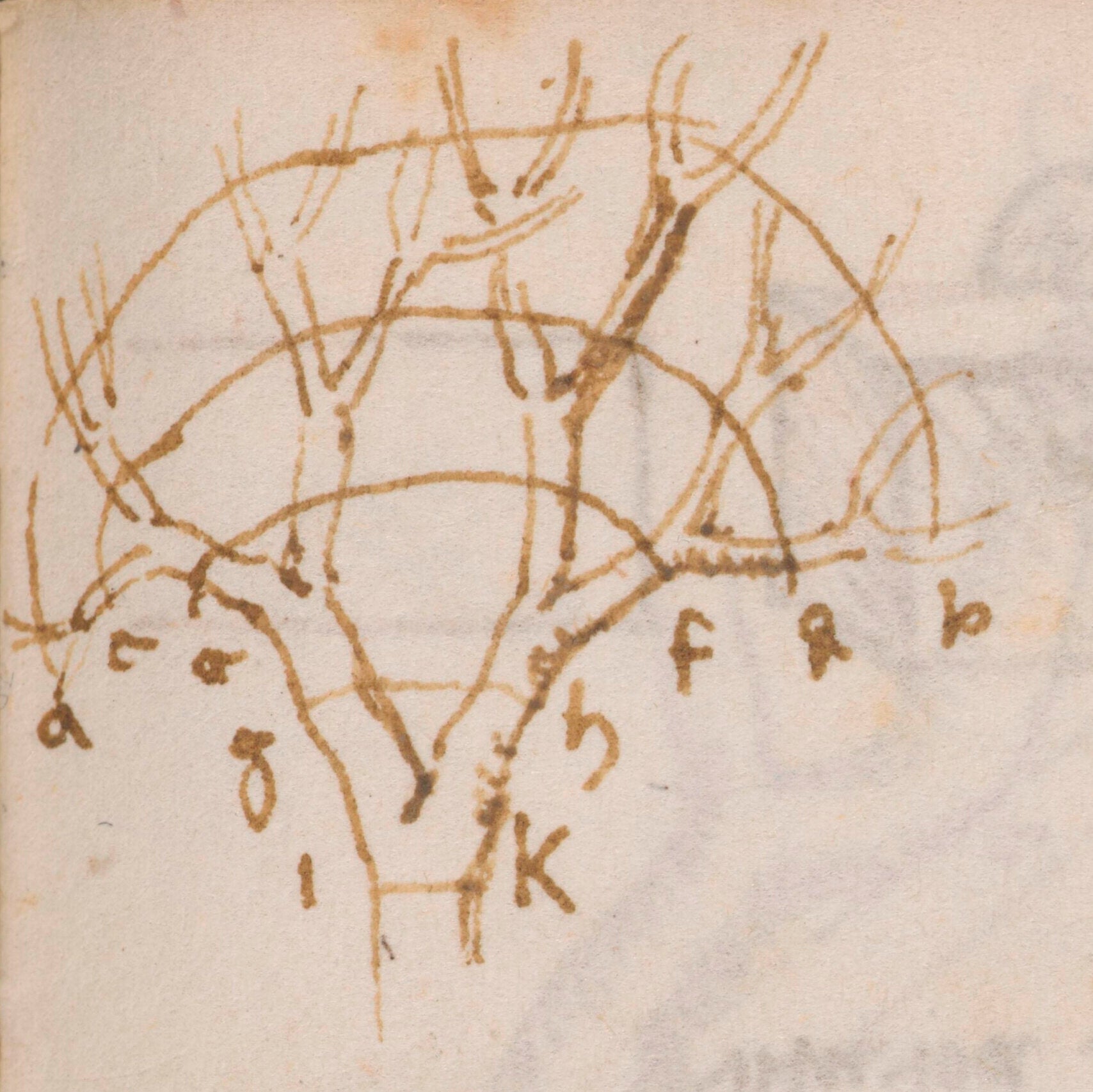
Leonardo da Vinci observed that tree limbs preserve their thickness as they branch.
The Italian Renaissance artist used a parameter called α to determine the relationships between the diameters of the various branches.
He asserted that if the thickness of a branch is the same as the summed thickness of its two smaller branches then the parameter α would be 2.
Researchers analysed trees in art from several parts of the world, including those in the 16th-century Sidi Saiyyed Mosque in Ahmedabad, India, Edo period Japanese painting, and 20th-century abstract art.

They found that the values of α in these artworks range from 1.5 to 2.8, similar to the range of this value in natural trees.
“We find α in the range 1.5 to 2.8 corresponding to the range of natural trees,” scientists wrote.
“While fractal dimension varies considerably across trees and artwork, we find that the range of α in case studies of great artworks across cultures and time periods corresponds to the range of real trees,” they said.

Even abstract paintings such as Piet Mondrian’s 1912 cubist Gray Tree, which doesn’t visually show treelike colours, can be identified as trees if a realistic value for α is used, researchers say.
“Abstract paintings with realistic α are recognisable as trees, whereas an otherwise similar painting is no longer distinctly recognisable as a tree,” they say.
The new study offers a perspective to “appreciate and recreate the beauty of trees,” scientists say.
It also highlights that art and science can provide complementary lenses on natural and human worlds, they added.


